Estadística--4 Ejemplos Coeficiente de correlación lineal de Pearson

 Coeficiente de correlación lineal de Pearson

Ejemplo1:

 Se hizo una tabla muestra de las alturas redondeadas en centímetros (cm) y pesados en kilogramos (Kg) de una muestra de 12 estudiantes del primer ciclo de Ingeniería Electrónica de la Universidad Privada Antenor Orrego. Nos piden determinar si existe relación entre los datos

Tabla Ejemplo1

Grafica del Ejemplo 1 Peso Y, Altura X

• Interpretación: Los datos muestran una pendiente ascendente, los datos se encuentran más alineados. 

 

Resumen del modelo
Modelo	R	R cuadrado	R cuadrado ajustado	Error estándar de la estimación
1	,866a	,749	,724	3,66823
a. Predictores: (Constante), Altura cm

• El coeficiente de Pearson: es cercano a 1 eso nos indica que es una correlación fuerte de los datos.

• El R cuadrado es de 74.9%

ANOVAa
Modelo		Suma de cuadrados	gl	Media cuadrática	F	Sig.
1	Regresión	402,110	1	402,110	29,884	,000b
	Residuo	134,559	10	13,456
	Total	536,669	11
a. Variable dependiente: Peso Kg
b. Predictores: (Constante), Altura cm

El error significativo es 0 por lo tanto se rechaza la hipótesis nula. Haciendo que R sea significativo.

Ejemplo 2:

Se realizó una tabla de muestra sobre el consumo de lejía en la tienda macro durante el mes de diciembre, con un stock de 1000 unidades de 2 litros de litros cada envase. Hallar el coeficiente de Pearson de la pendiente.

Tabla Ejemplo2

Resumen del modelo
Modelo	R	R cuadrado	R cuadrado ajustado	Error estándar de la estimación
1	,993a	,986	,983	1,39336
a. Predictores: (Constante), Stock

• Interpretación: Los datos muestran una pendiente ascendente, los datos se encuentran más alineados. 
• El coeficiente de Pearson: es cercano a 1 eso nos indica que es una correlación fuerte de los datos.
• El R cuadrado es de 98.6%

 

ANOVAa
Modelo		Suma de cuadrados	gl	Media cuadrática	F	Sig.
1	Regresión	661,150	1	661,150	340,544	,000b
	Residuo	9,707	5	1,941
	Total	670,857	6
a. Variable dependiente: Días
b. Predictores: (Constante), Stock

• El error significativo es 0 por lo tanto se rechaza la hipótesis nula. Haciendo que R sea significativo.

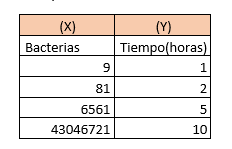
Grafica Ejemplo 2 

Ejemplo 3:

Se ha creado una tabla de muestra de la cantidad de bacterias en una placa petri de ensayo durante 10 horas.

Resumen del modelo
Modelo	R	R cuadrado	R cuadrado ajustado	Error estándar de la estimación
1	,907a	,823	,735	11082333,700
a. Predictores: (Constante), Horas

Interpretación: Los datos muestran una pendiente ascendente, los datos se encuentran más alineados. 

El coeficiente de Pearson: es cercano a 1 eso nos indica que es una correlación fuerte de los datos.

El R cuadrado es de 82.3%

ANOVAa
Modelo		Suma de cuadrados	gl	Media cuadrática	F	Sig.
1	Regresión	1143985781270207,000	1	1143985781270207,000	9,314	,093b
	Residuo	245636240492401,060	2	122818120246200,530
	Total	1389622021762608,000	3
a. Variable dependiente: Bacterias
b. Predictores: (Constante), Horas

Ejemplo 4:

Se ha creado una tabla de muestra de consumos de los helados Pezi_Duri Sabor Camu Camu durante el mes de Enero del 2021. Las ventas de un stock de 1600 unidades y se vendieron durante 30 días. Hallar el coeficiente de Pearson de la pendiente. 

Resumen del modelo
Modelo	R	R cuadrado	R cuadrado ajustado	Error estándar de la estimación
1	,934a	,872	,847	4,137
a. Predictores: (Constante), Stock

Interpretación: Los datos muestran una pendiente ascendente, los datos se encuentran más alineados. 

El coeficiente de Pearson: es cercano a 1 eso nos indica que es una correlación fuerte de los datos.

El R cuadrado es de 87.2%

ANOVAa
Modelo		Suma de cuadrados	gl	Media cuadrática	F	Sig.
1	Regresión	585,272	1	585,272	34,192	,002b
	Residuo	85,585	5	17,117
	Total	670,857	6
a. Variable dependiente: Días
b. Predictores: (Constante), Stock

Grafico Ejercicio 4